Funny question will you say. But with the output of Vue 3, in the end of 99, many new users appeared on the forums devoted to Vue, and amongst other things put the question to know how to get rid of the rings and ovals which appeared by using materials like " Checker" on spheres. Here is a pretence of answer:

Indeed, if you put side by side a sphere and a cube with textured with "Checker" from the "basic" section, you will have the following result:

(Note that this texture "Checker", has the notched box "object space" what means that it is centered on the origin of the object and that it follows it in its displacements.)

We can observe that the sphere has odd rounds, as if texture did not want to apply correctly to the sphere.

First stage: essential concepts

Well, all is in the manual (between us, one of best instruction manual than I ever had between my hands), but it appears that there are some who are allergic to any form of printed literature ;-).

• The primitives of Vue (sphere, cube, etc) are mathematically defined forms, and are not made of polygons, you can try to zoom as far as you want on a sphere, you will never see the least facet.
• Basicaly, procedural textures are to be opposed to mapped textures. The principal advantage of procedural textures (i.e. mathematically calculated), is their resolution (no pixellisation), their disadvantage is the increase in render times with their increasing complexity.
• Procedural textures are calculated starting from the origin of the world (X=0, Y=0, Z=0), or starting from the coordinates of the object if the box "object space" is notched.
• What one sees of a texture as "Checker" is the result of the intersection of this texture (which exists in 3D space), with the primitive or the object to which it is applied. To prove this, a small animation of a cube when the box "object space" is not notched, the cube "crosses" the texture:

Thus veiled the explanation of the circular drawings on the sphere: they are the "slices" made by the sphere on the texture checker .

Second stage: creation of the spherical chess-board

Let us peel a little the texture "Checker". It is based on the "rectangular" function. As we saw, such a function is not adapted if one wants to apply it to a sphere.

The solution is to use the function "Radial sine".

Here the step by step procedure:

1. Make a new scene with the atmosphere of your choice, hit Shift+S: that creates a sphere in the scene.
2. Edit the material of the sphere. In the edition window click on "New".
3. Change its name for "Checker sphere" for example; as you are in the top of window, notch "object space".
4. Let us go down, it is necessary to notch "Procedural Colors". By default, the colour gradation which appears goes from black to white, wich is perfect for our example.
5. Let us edit the function now (right-click on the small sphere to the left).
   
   
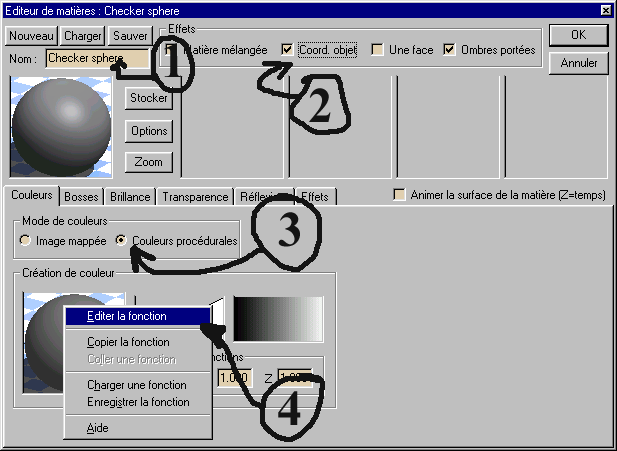
6. It is now necessary to change the "Null" default function into "Radial Sine". As the transition from the black to the white is done gradually, we need a filter to change that.
7. Load (right-click on the filters part) the filter "Step 50%" in the saturation collection. We now have an abrupt transition between black and white.
8. Good, that starts to take form, but the function gives results much too large. One reduces it by specifying X=0.1, Y=0.1 and Z=0.1 in the scale part (observe in real time the changes that that causes in the previsualisation window ).
   
   
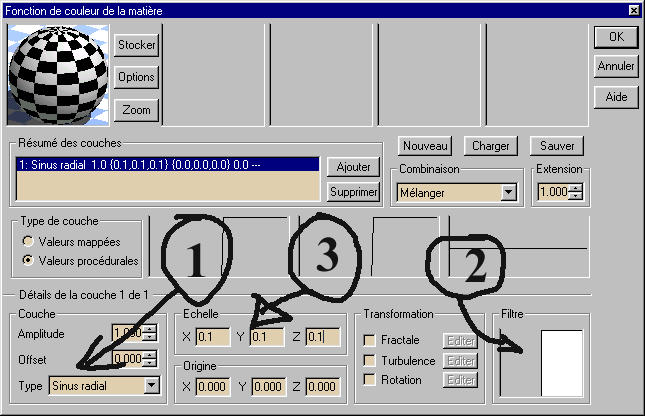
9. Voila, we have obtained our spherical chess-board, just do a test render. You will probably have to reduce the scale of texture to 0.3, depending of the size of the boxes you want.
   

Conclusion:

This tutorial is rather basic (and probably boring) and will not learn anything to the experts. For the other, it light a little I hope, the way in which a texture interract with the object onto which it is applied, one see also the importance of filters. By modifying some parameters here and there: here the kind of thing which one can obtain: